Una delle più recenti teorie che tenta di spiegare il comportamento dei mercati finanziari si basa su un concetto preciso, il caos. Parrebbe un ossimoro ma in realtà la teoria del caos è molto interessante.
Per iniziare dobbiamo metterci d’accordo sul significato da dare al termine caos. L’accezione che a noi interessa è squisitamente matematica. Il caos è sostanzialmente un processo non lineare, deterministico e dinamico. Cosa significa? Il caos è un processo nel quale il passato governa il futuro (deterministico) in maniera non proporzionale (non lineare) e che si modifica in ogni istante (dinamico).
Sin dagli anni 60 alcuni scienziati hanno iniziato a considerare quel mondo lineare, frutto della scienza classica, come una eccezione rispetto ad una natura delle cose che si muoveva, invece, in maniera caotica. Una delle caratteristiche fondamentali della teoria del caos è la forte dipendenza di un sistema dalle sue condizioni di partenza. L’implicazione principale di questo è che, allontanandoci dal punto iniziale, gli stati futuri diventano sempre meno prevedibili.
Piccole – e all’apparenza innocue – variazioni nel breve termine possono portare a risultati futuri semplicemente imprevedibili. Un esempio riconosciuto di sistema caotico è quello relativo al meteo. Un bel libro di James Gleick (Chaos, making a new science 1987) racconta il famoso episodio del meteorologo Edward Lorenz. Più poeticamente, tutti noi abbiamo sentito parlare dell’effetto farfalla, il cui battito di ali in un punto del globo terrestre potrebbe causare una tempesta in un altra zona del pianeta. Tutto dipende dalla fortissima relazione tra condizioni di partenza e sviluppo futuro di un processo.
Trasferendo la teoria del caos sui mercati finanziari si può dimostrare come, nel lungo periodo, il loro comportamento non sia prevedibile e che solo su orizzonti temporali molto brevi si possano calcolare valori e rendimenti attesi.
Uno dei lavori più interessanti sull’argomento è quello di Peters (1996). Il suo modello di mercato finanziario “caotico” ipotizza che il prezzo di una azione sia legato ad una funzione della domanda (ossia al fatto che, all’aumento di x di compratori, il prezzo sale di un determinato coefficiente a) meno l’effetto dovuto alla presenza di venditori (che tende ad abbassare il prezzo). Matematicamente Peters scrive la funzione di prezzo in questi termini:
Pt+1 = a * Pt(1-Pt)
Il prezzo al tempo t+1 è pari alla funzione della domanda a moltiplicata per Pt(1-Pt), dove Pt è il prezzo al tempo t.
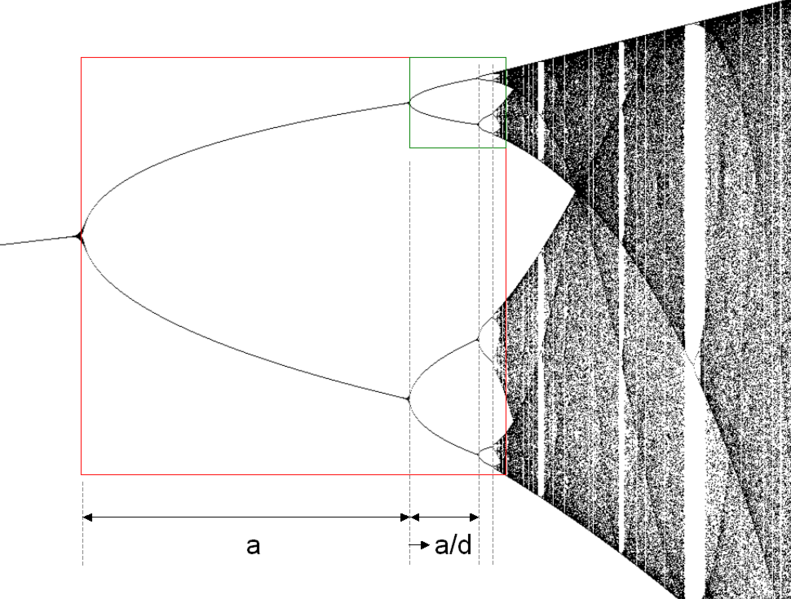
Simulando una contrattazione con differenti coefficienti a (ad esempio con a = 2 e a = 3), si ottiene un andamento dei prezzi imprevisto; graficamente otteniamo un diagramma biforcuto. L’equazione di Peters dimostra come piccolissime variazioni della funzione della domanda possano creare variazioni sui prezzi assolutamente non prevedibili.
La teoria del caos sembra apparentemente mettere in crisi le teorie lineari del mercato, che partono dall’ipotesi che il mercato agisca con schemi razionali. In realtà la teoria del caos può essere un interessante aiuto alle teorie tradizionali, riuscendo a spiegare fenomeni che sfuggono a queste ultime. I crolli dei mercati e la loro intensità, le anomalie di distribuzione statistica e molti altri aspetti dell’analisi finanziaria possono trovare nel caos una spiegazione plausibile.
La suggestione più interessante riguarda il fatto che i sistemi caotici non sono casuali ma possono presentare una certa ciclicità, cosa non prevista dai modelli tradizionali. Come possiamo attenderci che in estate le temperature siano più alte che in inverno, così possiamo – attraverso la teoria del caos – ipotizzare delle tendenze relativamente ai rendimenti di un mercato finanziario.